Statistics:

 

Types of data:

Categorical:

Qualitative

-        Nominal

·      Labelled

·      No quantity or order
(e.g. black, white, Hispanic)

-        Ordinal

·      Numbered

·      Variable increments
(e.g. mild, moderate, severe)

Numerical:

Quantitative

-        Discrete

·      Whole numbers only
(e.g. number of admissions)

-        Continuous

·      Any value

·      Constant increment

·      Interval data: false zero point (i.e. 20°C isn’t twice as hot as 10°C)

·      Ratio data: true zero point (e.g. 2/52 is twice as old as 1/52)

 

Test selection:

 

2 groups

>2 groups

Paired

Unpaired

Paired

Unpaired

Parametric

Student T

Student T

ANOVA

ANOVA

Non-parametric

-Nominal

McNemar

Chi

Cochrane Q

Cochrane Q

Non-parametric

-Ordinal / ratio

Wilcoxon Rank Sum

Mann Whitney U

Friedman

Kruskell Wallis

N.B. Parametric tests are used when data a) are numerical b) follow a distribution

 

Measures of central tendency:

Mean

·      Sum / number of observations

·      More affected by outliers

Median

·      Half the observations are higher, other half are lower

·      Less affected by outliers

Mode

·      Most frequently occurring value

·      Rarely relevant

 

Measures of spread:

Inter-quartile range

·      Middle 50% of observations

·      Often represented on box and whisker plot

o  Box: 25, 50 and 75

o  Whiskers: 10 and 90

Standard deviation

·      SD = √variance

·      Variance = ε(x-ẋ)2/(n-1), where
x: mean
ẋ: each value
n-1: degrees of freedom

Standard error

·      SE = SD/√n, where
n: number of observations

·      Indicates how far the sample mean is likely to be from the true mean

·      Used to derive confidence interval

Confidence interval

·      CI = mean ± z(SD/√n)
(where z is usually 95%)

·      Indicates a range within the true value is likely to fall

·      Indicates both magnitude and certainty of difference (cf. P value)

·      If the confidence interval crosses 1.0, result is insignificant

·      Can be calculated for anything: mean, odds ratio, relative risk etc

 

Comparisons:

Example:

 

Pain

No pain

Fentanyl

A

B

Nothing

C

D

 

Relative risk

·      Risk of pain in fentanyl group = A/(A+B) = RF

·      Risk of pain in nothing group = C/(C+D) = RN

·      Relative risk = RF/RN

·      The risk of the event in the intervention group compared with the risk of the even in the control group”

·      Amplifies the apparent effect of a drug on rare outcomes

o  e.g. if 1% to 0.3%: RRR is 70%, ARR is 0.3%

Odds ratio

·      Odds of pain in fentanyl group = A/B = OF

·      Odds of pain in nothing group = C/D = ON

·      Odds ratio = OF/ON

·      “A ratio of event to non-event in the intervention group compared with the control group”

·      Almost the same as RR if large data set and rare event

Hazard ratio

·      Hazard ratio is the relative risk of an event happening at time t

·      i.e. risk of pain now cf. risk of pain at some point

Number needed to treat

·      Absolute risk reduction = RN - RF

·      NNT = 1 / (absolute risk reduction)

 

Uncertainty:

Type 1 error

·      False positive

·      Threshold (α value) usually set 5%
(since inappropriately finding a difference is dangerous)

Type 2 error

·      False negative

·      Threshold (β value) usually set at 20%
(since inappropriately finding no difference is just unfortunate)

Power

·      The ability to detect a difference if there is one

·      Power = 1 – β value = usually 80%

Determinants:

·      Sample size (for 2x precision, need 4x numbers)

·      Magnitude of difference

·      Threshold for effect

·      (many others)

P value

·      Probability of finding this result (or greater) by chance if the null hypothesis were true

·      i.e. probability of this being a false positive result

Problems with p = 0.05

·      No account of prior probability

·      No indication of effect size

·      Not low enough if the stakes are high

·      Inappropriate for multiple comparisons (see Bonferroni correction)

Fragility index

·      Number of patients whose change in status would turn a significant result into a non-significant result

Bonferroni correction

·      Used if assessing for several outcomes simultaneously

·      Divide α (p = 0.05) by the number of tests being performed

Rule of 3’s MCQ

·      If no events in the entire population, 95% confidence interval is <3

·      Applies no matter how many in the population

·      Derived from binomial theory

 

Screening vs diagnostic tests:

 

Screening

Diagnostic

Target

Everyone

Symptomatic; or

Positive screening test

Nature

Non-invasive

Invasive

Thresholds

High sensitivity (few false neg)

High specificity (few false pos)

Cost

Cheap

Expensive

 

Screening tests: table

 

Difficult ETT

Not difficult ETT

Predictive values:

High MP score

a)True +ve

b)False +ve

PPV: a/(a+b)

Low MP score

c)False -ve

d)True -ve

NPV: d/(c+d)

 

Sensitivity: a/(a+c)

Specificity: d/(b+d)

 

 

 

 

 

 

·      Positive LR = sensitivity / (1-specificity)

·      Negative LR = (1-sensitivity) / specificity

 

 

 

 

Screening tests: definitions

Sensitivity

·      If have disease, how likely is the test to agree

·      SNOUT: SeNsitive test when negative rules OUT the disease

Specificity

·      if don’t have disease, how likely is the test to agree

·      SPIN: a SPecific test when positive rule IN the disease

PPV

·      If test says yes disease, how likely to have disease

·      ∝ prevalence as well as test quality

NPV

·      If test says no disease, how likely to not have disease

·      ∝ rareness as well as test quality

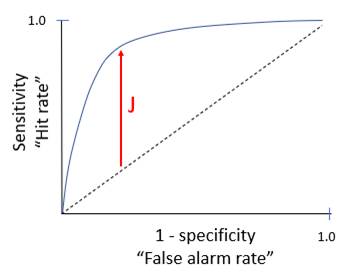
Receiver operator characteristic

·      Relationship between sensitivity, specificity, test quality

·      ↑AUC associated with high utility

Chart Description automatically generated with medium confidence

Youden’s J statistic

·      J = sensitivity + specificity - 1

·      J = point of maximum divergence of the curve

·      Single representation of a test’s utility, between 0 to 1

 

 

Feedback welcome at ketaminenightmares@gmail.com